Basic Hydrogeology

GROUND WATER, AQUIFERS, and CONFINING BEDS

Aquifer - "A water-bearing layer of rock, or of unconsolidated sediments, that will yield water in a usable quantity to a well or spring." Confining Bed - "A layer of rock, or of unconsolidated sediments, that retards the movement of water in and out of an aquifer and possesses a very low hydraulic conductivity." From these definitions, all rocks can be thought of as either aquifers or confining beds. Moreover, aquifers are often considered to be unconfined or confined. An aquifer is considered unconfined if water only partially fills the aquifer materials and water freely rises and declines along the unsaturated/saturated zone boundary. These unconfined aquifers are often referred to as water-table aquifers and wells that are opened to these unconfined aquifers indicates the position of the water-table. A confined aquifer is generally defined when water completely fills the aquifer materials and is overlain by a confining bed. A common term for a confined aquifer is an artesian aquifer. The water level from a well that permits water solely from a confined aquifer to enter the well will stand at some point above the top of the confined aquifer but not necessarily above the land surface. The water level in a well open to a specific confined aquifer stands at the level of the potentiometric surface. If the potentiometric surface is above land, the well is often considered as a free-flowing artesian well.

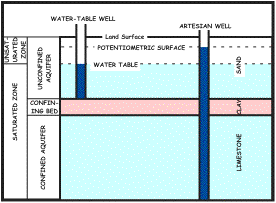Reference: modified from Heath (1993)

Our understanding of porosity provides us the ability to quantify the volume of water contained in our aquifers. Porosity is best understood as the ratio of the voids to the total volume of an unconsolidated or consolidated material.

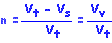Note: n = porosity as a decimal fraction Vt = the total volume of a material Vs = the volume of the solids in the material Vv = the volume of the voids Often, porosity is expressed as a percentage by multiplying the ratio by 100. Porosity also depends on the range of grain size (sorting) and shape of the subject material, but not on the size. Fine-grained materials tend to be better sorted than coarse-grained materials, thereby exhibiting greater porosities.

By looking at the above table one might conclude that fine-grained materials have the greatest ability to supply water to a well. This is not the case because physical properties such as adhesion (the molecular attraction of two different substances) and cohesion (the molecular attraction of similar substances) limit an aquifer's ability to release water into a well. Water stored in an aquifer that is retained as a film on the aquifer material or in very small openings is called specific retention. Conversely, water stored in an aquifer that will drain under the influence of gravity is called specific yield. The term effective porosity is often used to describe specific yield. With concepts of specific yield and retention in mind, let's look at our porosity chart once again.

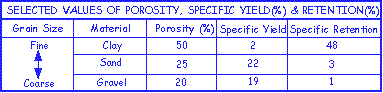As we can conclude, finer-grained materials such as clay have a high porosity but also have a high specific retention and low specific yield when compared to their coarse-grained counterparts, thereby limiting its ability to provide water to a well.

As previously discussed, water entering an unconfined or confined well will stand at a particular level. This level is often termed as the hydraulic head and is actually the sum of three components - the pressure head, elevation head and velocity head. The velocity head is often disregarded because ground water movement in most cases is relatively slow. In practical applications, a depth to ground water measurement is obtained and subtracted from the top of the well casing elevation to measure total head. Note that the datum plane illustrated below is often calibrated to sea level.

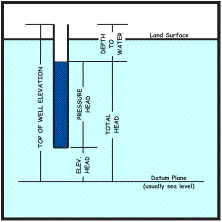When ground water level measurements are collected for a specific aquifer and contoured in a map perspective, a ground water surface map can be generated. Remember, water level measurements obtained from an unconfined aquifer represents the water table surface, and represent the potentiometric surface for water levels obtained from a confined aquifer.

The direction of ground water movement can be understood in the fact that ground water always flows in the direction of decreasing head. The rate of movement on the other hand is dependent on the hydraulic gradient, which is the change in head per unit distance. The change in head measurement is ideally in the direction where the maximum difference of head decrease occurs. In the example below, the hydraulic gradient is determined to be .00641 ft./ft. (the change in head divided by the change in distance). Notice the units are foot by foot but can be described in more inconsistent units such as foot per mile.

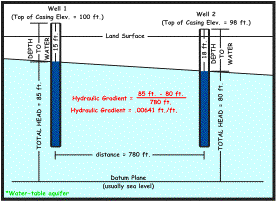Reference: modified from Heath (1993)

The direction and hydraulic gradient can be determined if the following data are available for three wells located in a triangular pattern. (1) Relative geographic position of the wells. (2) Distance between wells. (3) Total head (ground water level) at each well. The solution is outlined and illustrated below. (a) Identify the well that has the intermediate water level. (b) Calculate where the elevation of the well with the intermediate head would fall along a straight line between the wells having the highest and lowest heads. (c) Draw a straight line from the well with the intermediate head to its elevation equivalent plotted along the straight line between the wells having the highest and lowest heads. This line represents a segment of the water-level contour whereby the total head is the same as the intermediate well (d) Draw a line perpendicular to the water-level contour line just plotted with the well of highest or lowest head. This line is the line that parallels ground water direction. (e) Now, calculate the difference between the head of the well and that of the intermediate head contour by the distance between the well and the contour to reveal the hydraulic gradient. Thus, ground water flow direction is towards the south east at a hydraulic gradient of .00641 ft/ft.

The direction and hydraulic gradient can be determined if the relative geographic position, distance between wells and total head are available for three wells located in a triangular pattern. The solution is outlined and illustrated below (Heath, 1993). (a) Identify the well that has the intermediate water level. (b) Calculate where the elevation of the well with the intermediate head would fall along a straight line between the wells having the highest and lowest heads. (c) Draw a straight line from the well with the intermediate head to its elevation equivalent plotted along the straight line between the wells having the highest and lowest heads. This line represents a segment of the water-level contour whereby the total head is the same as the intermediate well (d) Draw a line perpendicular to the water-level contour line just plotted with the well of highest or lowest head. This line is the line that parallels ground water direction. (e) Now, calculate the difference between the head of the well and that of the intermediate head contour by the distance between the well and the contour to reveal the hydraulic gradient.

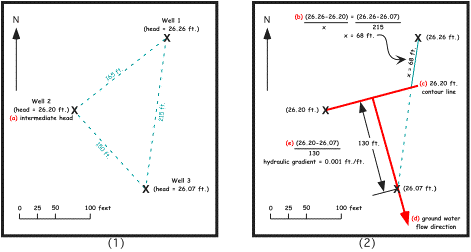Thus, ground water flow direction is towards the southeast at a hydraulic gradient of 0.001 ft/ft.

In the mid-1800s the French engineer Henry Darcy successfully quantified several factors controlling ground water movement. These factors are expressed in an equation that is commonly known as Darcy's Law.

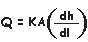By rearranging Darcy's Law and solving for hydraulic conductivity (K) in common units we can get a sense of what hydraulic conductivity really represents.

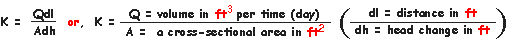Thus, in practical terms hydraulic conductivity is the volume of water flowing through a 1 ft. x 1 ft. cross-sectional area of an aquifer under a hydraulic gradient of 1 ft./ 1 ft. in a given amount of time (usually a day). If we cancel out our units, we see that hydraulic conductivity is usually expressed in ft./day.

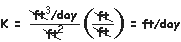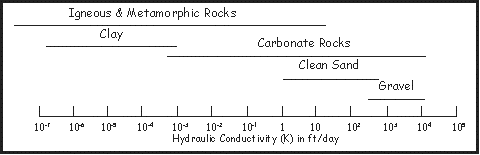
Hydraulic conductivity ranges approximately 12 orders of magnitude depending upon differing water transmitting characteristics of aquifer materials. As one may conclude from the chart below, the volume of water that can flow from our sandy and cavernous carbonate aquifer materials of the coastal plain are in most cases far greater than our rocks within the Piedmont and Blue Ridge provinces.

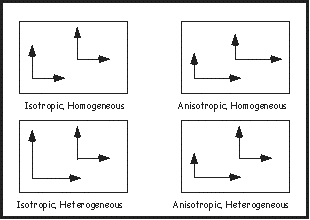
There are also some other terms used when regarding the spatial distribution of hydraulic conductivity within an aquifer. If the value of hydraulic conductivity is the same in all directions, the the aquifer is said to be isotropic. If hydraulic conductivity is different in different directions, the aquifer is said to be anisotropic. The terms homogeneous and heterogeneous are used when comparing hydraulic conductivity at separate locations of the aquifer, regardless whether the value is the same or different in all directions. The aquifer is homogeneous if hydraulic conductivity is the same and heterogeneous if different. The diagram below shows the four possible combinations when describing the hydraulic conductivity of aquifers.

Another important factor controlling ground water movement is its velocity. The ground water velocity equation can be derived from a combination of the velocity equation of hydraulics and our familiar friend, Darcy's Law.

We can solve for ground water velocity by; 1. substituting discharge (Q) by the cross-sectional area at a right angle to flow direction (A) times velocity (v) and, 2. cancelling our units. When we do this we discover that velocity (v) is equal to hydraulic conductivity (K) times hydraulic gradient (dh/dl).

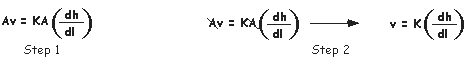In practical terms we know that ground water does not move in open space, rather it moves through aquifer materials that impedes ground water velocity. To account for this we need to include effective porosity (specific yield) to accurately quantify ground water velocity. Remember, hydrogeologists use effective porosity because this value better represents water flowing through an aquifer under the forces of gravity. Thus the velocity equation is modified.

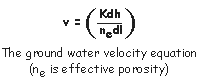Let's take a look at the difference of ground water velocity when comparing characteristics of a sandy substrate to that of a clay substrate. As we can see, ground water tends to move quicker in materials with higher effective porosities and hydraulic conductivities.

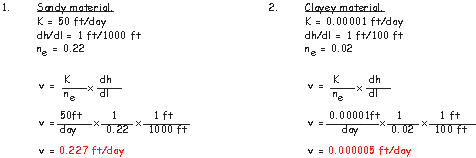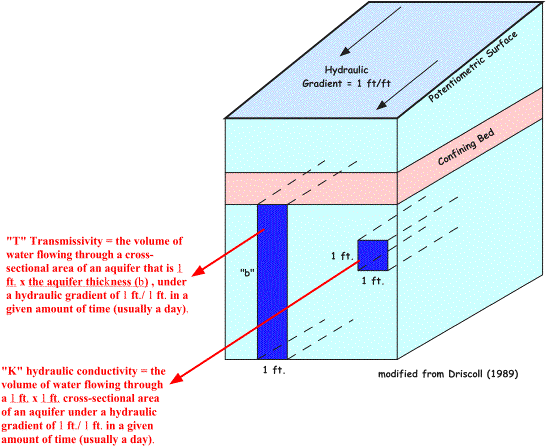
Transmissivity (T) is the volume of water flowing through a cross-sectional area of an aquifer that is 1 ft. x the aquifer thickness (b), under a hydraulic gradient of 1 ft./ 1 ft. in a given amount of time (usually a day). If we think about our definition of hydraulic conductivity, we can conclude that transmissivity (T) is actually equal to hydraulic conductivity(K) times aquifer thickness (b). Or otherwise denoted as T = Kb. We can also conclude that transmissivity is expressed as ft2/day because if T = Kb, then T = (ft./day)(ft./1). It is difficult to understand the differences between "T" and "K" when first introduced to these terms - the illustration below should hopefully bring it all together.

You'll often hear hydrogeologists speak of the "T" and "S" of aquifers. We now have an understanding of "T" or transmissivity. The "S" is used to represent the storage coefficient of an aquifer which is the volume of water released from an aquifer per 1 foot surface area per 1 foot change in head. Notice that we are not speaking of water flowing through an aquifer, rather we are referring an aquifer's ability to store water. Mathematically, the storage coefficient is dimensionless as the equation below illustrates.

The size of the storage coefficient is dependent whether the aquifer is unconfined or confined. In regards to a confined aquifer, water derived from storage is relative to; (1) the expansion of water as the aquifer is depressurized (pumped) and, (2) compression of the aquifer. In a confined aquifer setting, the load on top of an aquifer is supported by the solid rock skeleton and the hydraulic pressure exerted by water (the hydraulic pressure acts as a support mechanism). Because of these variables, the storage coefficient of most confined aquifers range from 10-5 to 10-3 (0.00001 to 0.001). Conversely, in an unconfined aquifer setting, the predominant source of water is from gravity drainage and the expansion of water and compaction of the rock skeleton is negligible. Thus, the storage coefficient is approximate to value of specific yield and ranges from 0.1 to about 0.3.

As water is withdrawn from a well, the water level in the well begins to decline as water is removed from storage in the well. The head in the well will fall below the level of the surrounding aquifer and water begins moving from the aquifer into the well. The water level will continue to decline and the flow rate of water into the well will increase until the inflow rate is equal to withdrawal rate. Water from the aquifer must converge on the well from all directions and the hydraulic gradient must get steeper near the well. For this reason the resultant 3-D shape of water withdrawal is a called a cone of depression.

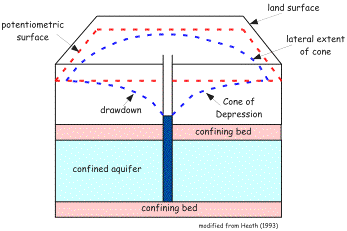The aquifer parameters of transmissivity (T) and storage coefficient (S) are variables that can dictate the shape of the cone of depression. Relative to a confined aquifer, the expansion of water in response to depressurizing (pumping) is very small, yet compression of the rock skeleton is great. This permits the cone of depression to expand and deepen rapidly when pumped. Thus, lower "S" values create deeper and wider cones than higher "S" value aquifers that do not deepen and expand as readily. In regards to transmissivity, aquifers of low "T" develop deep and narrow cones of depression and aquifers of high "T" area characterized by shallow and wide cones. The reasons for this are fairly complex and require more background information to be explained fully. However, think about the "T" relationship this way - a greater decline in hydraulic head would be required to move water through a less transmissive aquifer than a more transmissive aquifer.
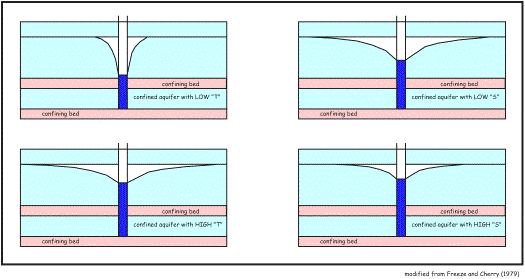